Попросили меня тут поделиться мнением о том, каким же должен быть размер партий в одном хорошо известном мне производстве. А я подумал, и решил, что на эту тему много чего можно сказать, поэтому решил записать, чтобы не забыть на потом.
Данная статья не претендует на то, чтобы дать всеобъемлющий ответ на вопрос об оптимальных размерах производственных партий, ее цель — собрать в одно месте некоторые аспекты одно из проблем планирования сложного производства.
Начнем с определения
Вообще, чтобы действительно правильно начать ответ, нужно дать определение производственной партии. И одна только эта попытка может вызвать к жизни несколько крестовых походов и священных войн между адептами того или иного подхода. По крайней мере, в те годы, когда я работал консультантом в консалтинговой компании, мы долго ломали копья по поводу этого определения, пока один из мудрых коллег не предложил 5 вариантов, которые бы более-менее закрыли всё множество вариаций производственных партий.
Партия — это:
- Размер заказа клиента – внешнего, или внутреннего (между операциями)
- Технологическая партия – одновременно обрабатываемое количество продукции
- Количество продукции, выпускаемое между переналадками
- Количество продукции, выпускаемой между транспортировками
- Объем накопителя или бункера, единовременно загружаемый перед операцией
В общем случае следует говорить о том, что производственная партия — это то количество деталей, изделий, продукции, которое обрабатывается на одном этапе производства без перерывов, остановок и переключения на другой тип деталей, изделий, продукции. Не могу сказать, что это лучшее определение партии, которое можно дать, но для целей этой статьи, думаю, его будет достаточно.
Экономически оптимальный размер партии на одной операции
Для каждого отдельного этапа производства можно достаточно достоверно определить экономически оптимальный размер партии, для чего используют формулу Уилсона
где EOQ — экономичный размер заказа (economic order quantity – EOQ)),
Q — количество товара в год (Quantity in annual units),
P — затраты на реализацию заказа (Placing an order cost),
C — затраты на складирование единицы товара в год (Carry costs)
или ее аналог формулу Андлера
где у min — оптимальный размер партии,
V — требуемый объем продукции за период времени (скорость сбыта),
Cr — затраты, связанные со сменой партий ( условно — на наладку),
Cl — удельные расходы на складирование в периоде времени.
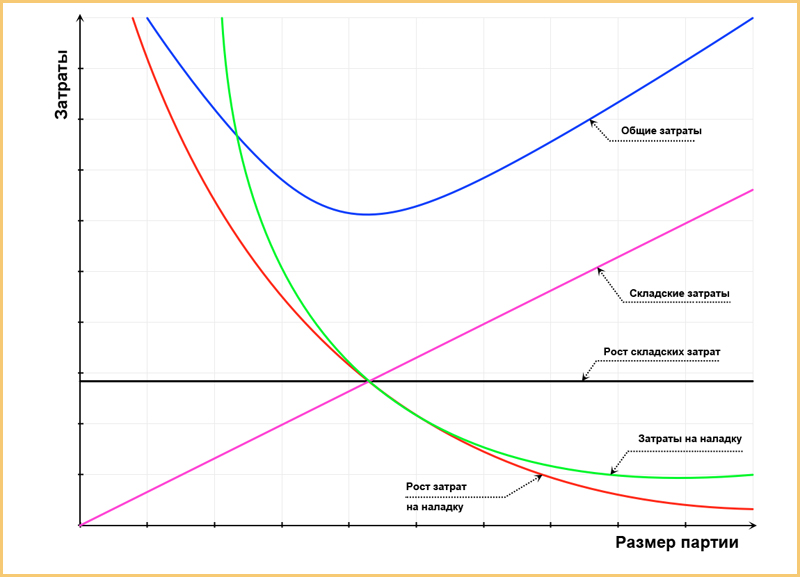
Общий вид графика таков:
Собственно, тут надо искать минимум кривой «Общие затраты», а значение Х, которое ему соответствует, и будет представлять собой «экономически оптимальный размер партии».
Естественно, это всё выглядит просто только на графике, чтобы посчитать точное значение, нужно хорошо понимать затраты на наладку (зеленая кривая) и величину складских затрат (сиреневая кривая).
В затраты на наладку могут попадать:
- стоимость простоя оборудования
- стоимость простоя операторов
- затраты на наладчиков
- затраты на инструмент
- затраты на оснастку
- дополнительные затраты материалов и энергоносителей на время останова/пуска
- и т.д.
В величину складских затрат попадают:
- стоимость хранимых объектов
- стоимость складских площадей
- затраты на складской персонал
- затраты на освещение и отопление
- затраты на складскую технику (штабелеры / погрузчики)
- и т.д.
В общем, достаточно много чего нужно учесть.
Кривая общих затрат не имеет излома в токе минимума, а это означает, что если вы получили, к примеру, экономически оптимальный размер партии в 1327 штук, то, скорее всего, вы можете запускать производство партиями от 1300 до 1400 штук без каких-либо существенных отклонений в себестоимости, ну и уж точно если оптимальный размер партии — 4,6 штуки, то можно запускать партии и по 4 штуки и по 5 штук.
Проблема: разные технологии — разные партии
Проблема реального производства заключается в том, что затраты на наладку и складские затраты неодинаковы на всём производственном цикле, и это вносит разногласия в то, каким должен быть размер партии, которая проходит несколько стадий производства, а не только одну.
Например, сырье выгодно привозить фурами, т.к. стоимость транспортного средства «размазывается» на весь объем сырья, сколько бы его ни было, термообработку нужно выполнять для такого количества деталей, которые максимально можно засунуть в печь, а отгрузку нужно делать только в том количестве, которое заказал конкретный заказчик, иначе всё лишнее, что вы ему отправите, просто достанется ему даром.
Хранить мелкие и объемные объекты тоже стоит разные деньги, а если какое-то сырье нужно еще и держать в тепле или других «особых климатических условиях», то стоимость хранения такого сырья будет выше, чем для других видов сырья.
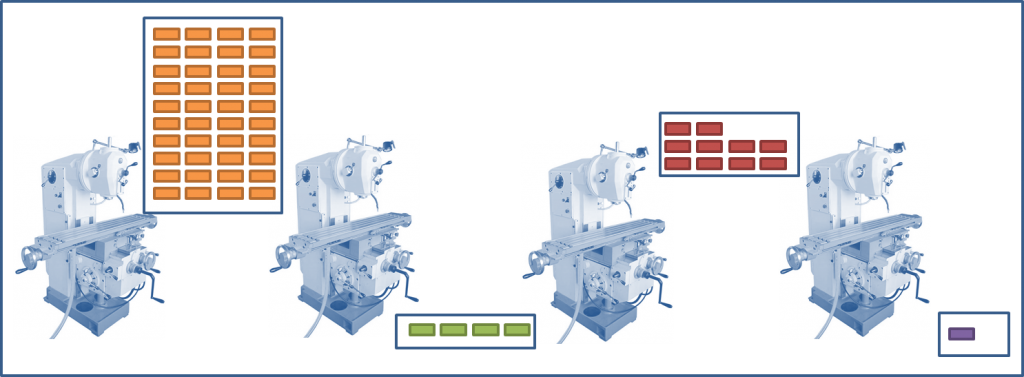
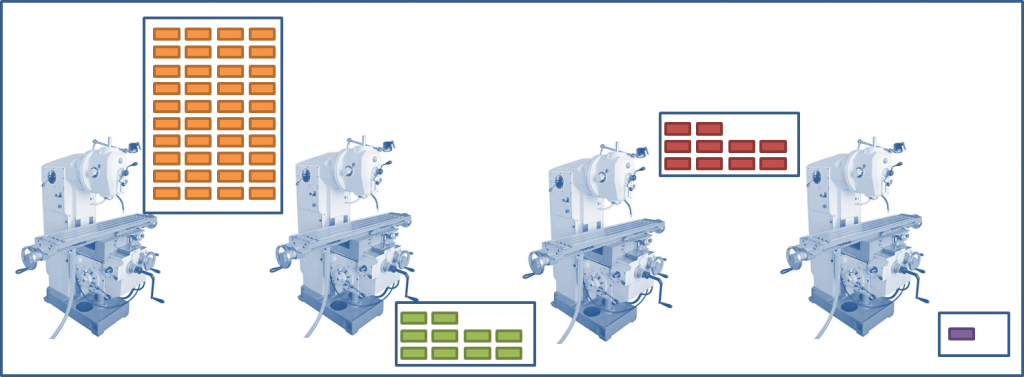
В итоге, если посчитать экономически оптимальный размер партии на четырех участках, можно получить, к примеру, такую картину (по порядку прохождения этапов производства):
- 2000 штук в партии
- 200 штук в партии
- 540 штук в партии
- 34 штуки в партии
И хорошо еще, если единицы измерений в каждом случае одинаковые. А то ведь может получиться и так:
- 2000 кг в партии
- 200 штук в партии
- 540 пар в партии
- 34 комплекта в партии
В этом случае проблема оптимального размера партии только усугубляется.
Крайние варианты решения проблемы
Чтобы не путаться хочется иметь один размер партии на все случаи жизни. Ведь если на одном этапе производства партия состоит из десяти штук, а на другом из тринадцати, нужно организовывать какой-то промежуточный склад для того, чтобы накапливать недостающие штуки полуфабрикатов.
Какие же могут быть крайние варианты?
Их два:
- использовать максимальный из расчетных размеров партий
- использовать минимальный из расчетных размеров партий
Возьмем пример со штуками, описанный выше (2000, 200, 530 и 34 штуки) и посмотрим, как на нем реализовать оба варианта.
Максимальный размер партии
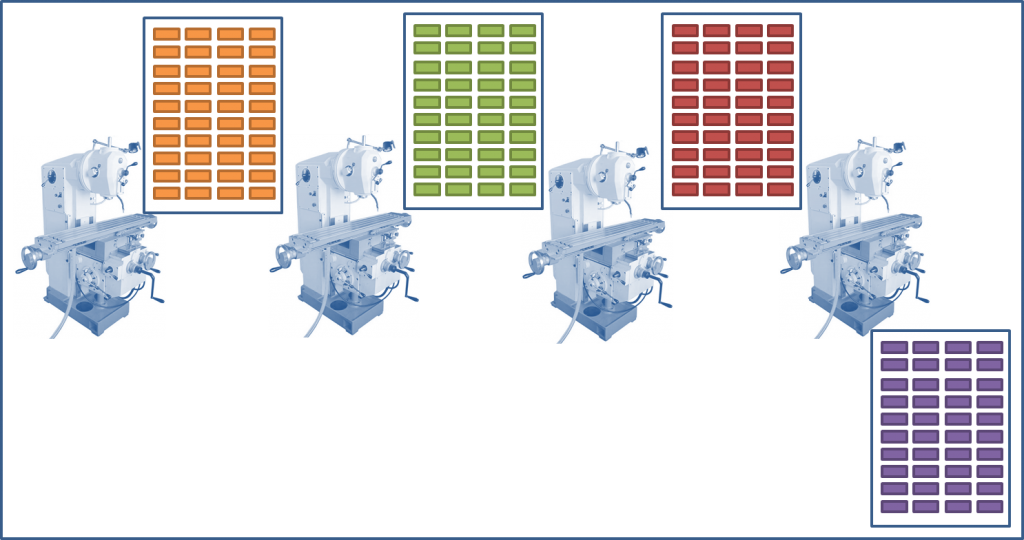
Максимальный размер партии из всех четырех вариантов — 2000 штук. Согласившись на его использование мы приходим к планированию производства, в котором используются только партии объемом 2000 штук:
- 2000 штук в партии
- 2000 штук в партии
- 2000 штук в партии
- 2000 штук в партии
Что при этом получается?
На первом этапе мы получаем оптимальный размер партии — ни больше, ни меньше. И те, кто работают на этом участке, а тем более те, кто им управляет, должны быть абсолютно довольны таким решением.
На втором этапе размер партии в 10 раз превышает оптимальный. Что это означает? Мы тратим в 10 раз меньше времени на переналадку этого этапа производства, но при этом заполняем промежуточный склад между 2 и 3 этапами большим объемом запасов, которые вдесятеро превышают то, что могло бы устроить наших менеджеров.
На третьем этапе размер партии больше оптимального почти в 4 раза, и это тоже может приводить к большому количеству запасов.
Но вот где запасов точно ОЧЕНЬ МНОГО — это после четвертого этапа. Там-то можно работать по 34 штуки, а это означает, что размер партии практически в 60 раз больше оптимального.
Чем хорошо и чем плохо такое решение.
Хороший результат заключается в том, что оборудование будет загружено по полной программе, простои на переналадку будут сведены к минимуму, и если мы сможем синхронизировать переналадку оборудования и пропускать по одной партии через все этапы по порядку, то нам нужно будет только три промежуточных склада на 2000 штук полуфабрикатов (между первым и вторым этапами, между вторым и третьим этапами, между третьим и четвертым этапами) и тогда весь процесс будет работать как конвейер. Если какой-то из этапов остановится, то ограничение в размер промежуточного склада в 2000 штук быстро вынудит остановить всё производство и перепроизводства не произойдет: последующие этапы исчерпают свои запасы полуфабрикатов и остановятся, т.к. аварийный этап не позволит их пополнять, а предыдущие этапы заполнят промежуточные склады и тоже остановятся, т.к. аварийный этап не позволит их освобождать).
Плохой результат в том, что вам скорее всего понадобится очень много складских площадей для организации трех промежуточных складов: чаще всего производство организуют так. что пока все 2000 полуфабрикатов не появятся на предшествующем складе, следующий этап производства не запускается, а это означает, что под эти полуфабрикаты нужно иметь соответствующее пространство (в отдельных случаях можно работать «с колес», т.е. запускать производство на следующем этапе еще до того, как вся партия в 2000 полуфабрикатов завершена, но это возможно не для каждой технологии). Хуже всего дело будет обстоять со складом готовой продукции, т.к. там мы получим катастрофический запас избыточной продукции.
Минимальный размер партии
Минимальный размер партии из всех четырех вариантов — 34 штуки. Согласившись на его использование мы приходим к планированию производства, в котором используются только партии объемом 34 штуки:
- 34 штуки в партии
- 34 штуки в партии
- 34 штуки в партии
- 34 штуки в партии
Что при этом получается?
На первом этапе переналадка будет выполняться в 60 раз чаще, чем этого требуется для оптимального варианта. Это очень много. Если каждая переналадка занимает ощутимое время, это может катастрофическим образом сказаться на производительности всего процесса — он просто не будет успевать выпускать всё, что вы хотите от него получить.
Дальше переналадка будет выполняться тоже неоптимально — в 6 раз чаще, чем это требуется для оптимального варианта. Хуже того, если, например, при запуске каждой партии используется дорогостоящая оснастка или материалы, которые расходуются один раз на всю партию, эти расходы существенно возрастут и лягут непомерным грузом на себестоимость продукции.
То же самое будет с третьим этапом, и только на четвертом этапе всё будет так как надо.
В общем случае, весь производственный процесс будет идти медленнее, его будет сдерживать этап с самой длительной переналадкой.
Плюсы данного варианта в том, что вы сводите к минимуму потребности в складских площадях — их нужно только столько, сколько требуется для хранения 3 видов полуфабрикатов по 34 штуки, еще немного — для 34 единиц сырья и 34 единиц готовой продукции. Микроскопическая цифра, по сравнению с предыдущим этапом.
Минусы — возросшие потери оснастки на переналадках и сократившаяся из-за больших потерь времени на переналадку производительность всего процесса в целом.
Давайте оставим всё как есть
Теперь, разобравшись с тем, что происходит в крайних случаях, можно разобраться, а как будет действовать производство, если оставить размеры партий такими, чтобы они были равны экономически оптимальному размеру партии каждого этапа в отдельности:
- 2000 штук в партии
- 200 штук в партии
- 540 штук в партии
- 34 штук в партии
Итак, как это будет работать?
Для запуска такого производства нам понадобится 2000 единиц сырья перед первым этапом. Тогда мы сможем выполнить наладку и запустить оптимальную партию в производство и всё будет хорошо.
После этого 2000 полуфабрикатов попадут на промежуточный склад. Из них за первый заход отберут только 200 штук, чтобы начать оптимальным образом второй этап производства. Здесь тоже всё хорошо.
После второго этапа 200 штук лягут в запас и будут ждать следующей партии, поскольку для запуска третьего этапа нужно не меньше 540 штук. И если второй этап будет изготавливать полуфабрикаты того же типа, то потребуется выпустить еще два партии по 200 штук. В этом случае запасы между вторым и третьим этапом достигнут 600 штук и можно будет запустить третий этап производства.
Третий этап производства выдаст 540 полуфабрикатов на последний промежуточный склад и они будут потребляться оттуда небольшими партиями по 34 штуки. В этом случае мы обеспечим минимальные запасы на складе готовой продукции, но всё равно не избавимся от запасов на складе полуфабрикатов между 3 и 4 этапами производства.
Что можно увидеть в этой ситуации?
Размер промежуточного склада пропорционален той из экономически оптимальных партий этих двух этапов, которая больше по количеству.
Т.е. склад полуфабрикатов между первым и вторым этапами производства должен вмещать не менее 2000 изделий. Склад полуфабрикатов между вторым и третьим этапами производства должен вмещать 540, а вовсе не 200 изделий. И склад полуфабрикатов между третьим и четвертым этапами производства тоже должен вмещать 540 изделий. Склад готовой продукции должен вмещать партии в 34 готовых изделия и этого, видимо, в нашем случае будет достаточно.
Интересно, что из этого вытекает первое изменение, которое стоит внести в систему планирования.
Поскольку размер складов у нас больше оптимального (2000, 540, 540 и 34), то нет никакого логического смысла запускать на втором этапе партии по 200 штук, а не по 540 — склад мы всё равно оплачиваем как «на 540» и накапливаем там детали для запуска на следующем этапе по (минимум) 540 штук, поэтому стоит изменить размер экономически оптимальной партии второго этапа с 200 на 540 несмотря на то, что цифру 200 мы получили расчетным путем по вышеприведённой формуле.
В реальности принятие такого решения выглядит так: мастер участка, на котором происходит выполнение второго этапа производства, смотрит на статистику запасов полуфабрикатов на обоих складах и говорит примерно следующее: «а чего мы вообще паримся и всё время переналадки делаем, это же никому не нужно!»
Таким образом, мы плавно переходим к варианту 2:
- 2000 штук в партии
- 540 штук в партии
- 540 штук в партии
- 34 штук в партии
И это не самоуправство, это — просто здравый смысл мастера или планировщика, потому что в данном случае работа партиями по 200 штук действительно не нужна ни для чего кроме для соответствия расчётному экономически обоснованному размеру партии. А если это не игровая ситуация, а жизненная, то на расчётные цифры всем наплевать — ведь очевидно, что в данном случае в расчёте не учли особенностей всего процесса целиком.
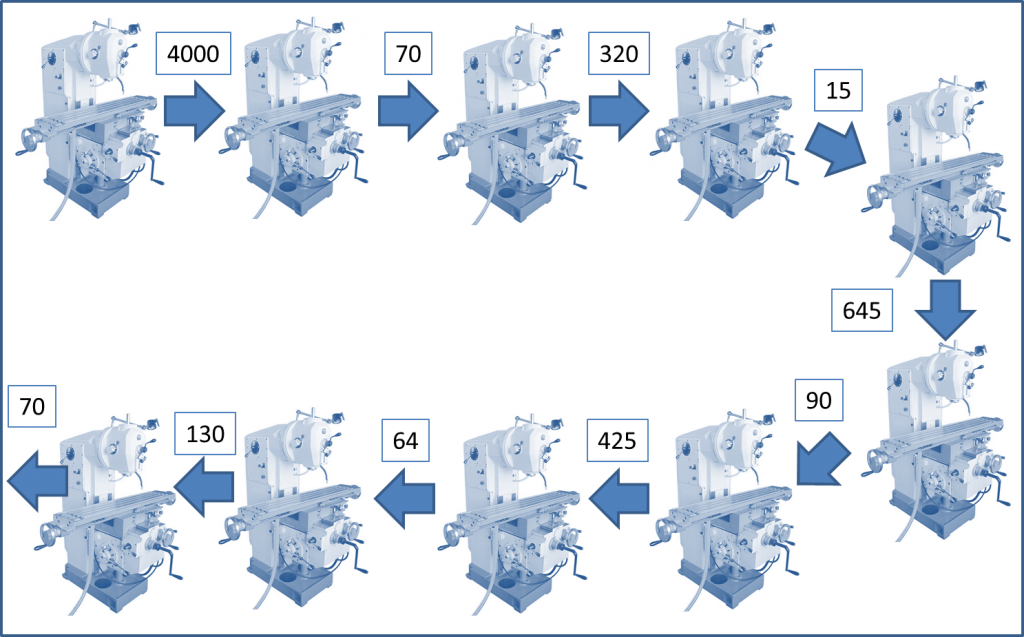
Чтобы продемонстрировать это подход другим примером, давайте предположим, что производство состоит не из 4, а из 10 этапов, и оптимальные партии для каждого этапа были рассчитаны следующим образом:
- 4000 штук
- 70 штук
- 320 штук
- 15 штук
- 645 штук
- 90 штук
- 425 штук
- 64 штук
- 130 штук
- 70 штук
Очевидно, что запасы между этапами должны вмещать не меньше чем:
- 4000 изделий между первым и вторым этапами
- 320 изделий между вторым и третьим этапами
- 320 изделий между третьим и четвертым этапами
- 645 изделий между четвертым и пятым этапами
- 645 изделий между пятым и шестым этапами
- 425 изделий между шестым и седьмым этапами
- 425 изделий между седьмым и восьмым этапами
- 130 изделий между восьмым и девятым этапами
- 130 изделий между девятым и десятым этапами
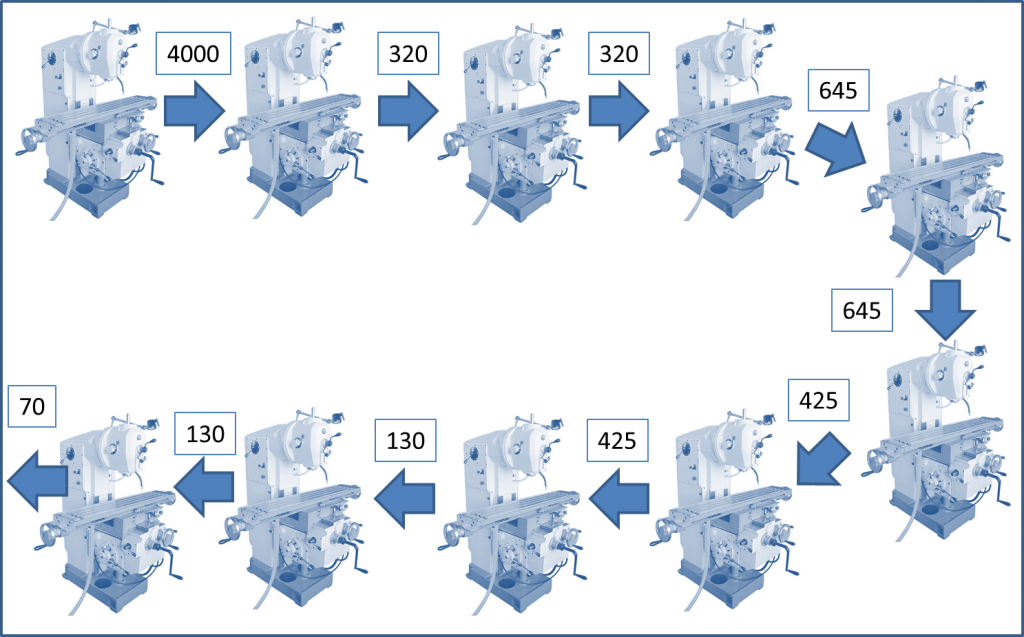
Поразмышляв немного над оптимальными размерами партий можно прийти к выводу, что с тем же успехом можно выставить размеры партий следующим образом:
- 4000 изделий
- 320 изделий
- 320 изделий
- 645 изделий
- 645 изделий
- 425 изделий
- 425 изделий
- 130 изделий
- 130 изделий
- 70 изделий
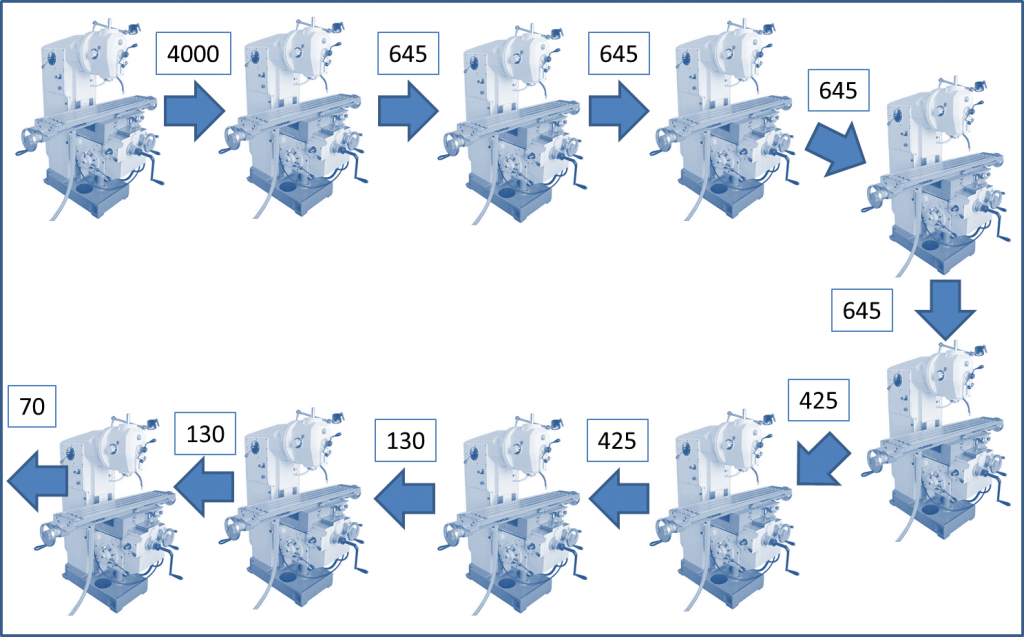
Теперь становится понятным, что между третьим и четвертым этапами нужен буфер в 645 изделий, а потом окажется, что такой же буфер на самом деле нужен и между вторым и третьим этапами производства. В итоге оптимальные размеры производственных партий по этапам будут составлять следующую последовательность:
- 4000 изделий
- 645 изделий
- 645 изделий
- 645 изделий
- 645 изделий
- 425 изделий
- 425 изделий
- 130 изделий
- 130 изделий
- 70 изделий
Т.е. в стабильном состоянии любой набор партий на этапах производства стремится к такому набору, когда на следующем этапе размер партии равен или меньше размера партии предыдущего этапа.
Давайте назовем это парадоксом «домашних консервных заготовок»: сначала мы собираем весь урожай, какой можем, и закатываем его по банкам, затем, по праздникам, достаем из запасов банку огурцов, открываем ее, и несколько дней поспешно доедаем открытую банку огурцов, чтобы они не испортились — на каждом этапе «потребления» урожая огурцов размер партии всё меньше и меньше, пока он не достигнет размера партий, которыми забирает продукцию потребитель.
Если бы у нас первоначально размеры партий составляли бы такую последовательность:
- 34 штуки
- 540 штук
- 200 штук
- 2000 штук,
то вполне разумно ожидать, что спустя какое-то время набор размеров партий пришел бы к варианту
- 2000 штук
- 2000 штук
- 2000 штук
- 2000 штук,
поскольку нет никакой необходимости 10 раз перенастраивать оборудование третьего этапа производства, чтобы запустить одну партию в 2000 одинаковых изделий на четвертом этапе.
Предупреждение о условиях, которые остались «за текстом»
Все эти расклады даны для одного типа изделий без учета других типов изделий — мы просто имеем в виду, что переналадка производится для изготовления «другого» типа продукции.
Парадокс «домашних консервных заготовок» в чистом виде можно увидеть только на том производстве, где производственных и складских площадей достаточно для хранения всех этих разрастающихся запасов. В противном случае они будут ограничиваться физическими масштабами производства, однако при этом суть парадокса будет такой же: размеры партий на предшествующих этапах будут увеличиваться до тех пор, пока не будет достигнут предел занимаемого запасами пространства, либо пока этот самый размер партий не достигнет размера партий последующих этапов.
Важный вывод о предельном оптимальном размере партии
Размер партий на каждом этапе производства будет не меньше размеров партий последнего этапа производства или последнего этапа транспортировки продукции заказчику.
Т.е. если вы отгружаете клиенту зубные велосипедные насосы сорокафутовыми контейнерами, нет никакого смысла производить их партиями по 10 штук, а не по 50 или по 1000 — в конечном итоге вам всё равно нужен будет полный контейнер насосов.
Расчет минимально допустимого размера партии
В логике бережливого производства одной из целью планирования производства является снижение размера партии вплоть до достижения идеального состояния, которое описывается понятием «поток единичных изделий» — One Piece Flow.
Если расчет экономически оптимального размера партий делается в рамках общепринятой логики управления, когда определенные размеры запасов являются благом, а не злом, то в бережливом производстве, когда любые запасы считаются в той или иной степени вредными, вопрос оптимального размера партий ставится немного иначе: насколько маленькими могут быть партии производства при условии сохранения необходимого уровня производительности производства?
Вот расчет.
Предположим, нам надо изготовить за время T определенное количество n изделий или полуфабрикатов. Среднее время цикла составляет CT. В этом случае время, которое мы можем потратить на переналадки будет равно
Tcho = (T — n x CT)
Если одна переналадка занимает примерно время величиной ChT, то мы можем позволить себе определенное количество переналадок за этот период времени:
Ncho = (T — n x CT) / ChT
И тогда среднее количество изделий в партии будет равно:
Batch = n / Ncho = n x ChT / (T — n x CT)
Для максимума выполняемых за определенный период времени переналадок это будет минимум изделий на одну партию, при котором производство еще успевает выполнить свой план.
Вот пример.
Длительность смены
T = 8 часов или 480 минут
Время цикла
СТ = 1 минута / изделие
Плановый выпуск
n = 400 изделий
Длительность переналадки
Tcho = 5 минут
Batch = 400 x 5 / (480 — 400 x 1) = 400 x 5 / 80 = 25 изделий (округляем вверх)
Для надежности стоит ввести коэффициент доступности оборудования, чтобы учесть время на обслуживание и ремонт.
Тогда формула будет выглядеть так:
Batch = n x ChT / ( T x k — n x CT )
в этом случае, если в наш пример добавить коэффициент доступности 90%, то размер партии будет равен:
Batch = 400 x 5 / (480 x 0,9 — 400 x 1) = 400 x 5 / (432 — 400) = 400 x 5 / 32 = 63 изделий.
Вот несколько следствий из этой формулы:
- Чем больше плановый выпуск, тем меньше можно сделать переналадок и тем больший размер партий нужно применять.
- Чем меньше коэффициент доступности, тем меньше переналадок и тем больше размер партий.
- Чем больше время переналадки, тем меньше переналадок и тем больше размер партий
- Чем меньше время переналадки, тем больше можно сделать переналадок и тем меньший размер партий можно использовать.
В данной формуле сделаны два упрощения с учетом следующих предположений:
n — общее количество всех изделий одного семейства, которые нужно сделать за данное время, станок выпускает только эти изделия и никакие другие.
CT — усредненное время цикла производства любого одного изделия данного семейства изделий.
Это всё замечательно, но каким должен быть размер партии?
Начнем с конца. Применив последнюю формулу из неэкономического расчета для последнего этапа производства, вы сможете посчитать тот самый предельный оптимальный размер партии.
Размеры партий на предыдущих этапах можно установить таким же образом.
Если для вас критична складская или производственная площадь, то нужно поставить объем партий на каждом этапе под контроль, как и то, сколько пространства занимают промежуточные запасы.
Если это не критично, то размеры оптимальных партий на промежуточных этапах можно увеличить как минимум до предельного оптимального размера партии (рассчитанного для последнего этапа).
Если есть еще возможности хранить запасы — вы можете использовать парадокс «домашних консервных заготовок» и выстроить размеры партий в ниспадающем порядке (от самых больших на первых этапах к предельно оптимальной партии на последнем этапе).
На каждом промежуточном складе между этапами, которые имеют одинаковые размеры оптимальных партий должно единовременно находиться не более одной такой партии продукции. И они должны проходить по таким складам и этапам в режиме FIFO — первый вошел, первый вышел.
Размеры промежуточных складов между этапами, для которых размер оптимальных партий отличается друг от друга, нужно так же установить максимальный допустимый объем хранения и, при возможности, ввести в действие тот же принцип FIFO, чтобы продукция сразу после накопления до нужного количестве попадала на следующий этап.
Сложный случай
Что делать в том случае, если изделия состоят из множества деталей, а самих видов изделий много и они выпускаются последовательно один за другим, перемежаясь переналадками оборудования?
Очевидно, нужно брать базовые модели расчетов и перекладывать их на новые исходные условия. В целом это весьма непростая задача, и дать для нее решение в общем виде в этой статье определённо не получится. Однако я надеюсь, что вышеизложенного будет достаточно для того, чтобы запустить процесс обсуждения деталей системы планирования для тех предприятий, которые пытаются найти для себя ответ на вопрос «какие же партии будут оптимальны для нашего производства».
Если у вас появились вопросы или замечания — вы можете оставить их в комментариях к статье, либо в контактной форме.
Фото взяты здесь, здесь, здесь и здесь.
Кому это может быть интересно
Узнать, кто эти люди…


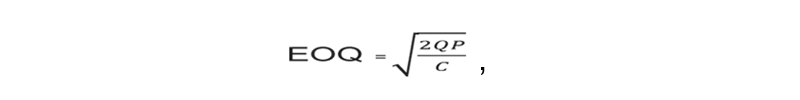














Здравствуйте в примере «не экономического » расчета откуда появилась выражение 450 *5
Олег, спасибо за комментарий. Это досадная ошибка. Должно быть 400 * 5, текст немного подкорректировал, чтобы было видно, какая величина чему равна в примере, расчеты исправил.